Persistent Poliglocy Paradox
- Processes, standards and quality
- Technologies
- Others
Usually, we have to make important decisions at the beginning of the project. It is unfortunate, as at the time we have limited knowledge about the domain. The uncertainty leads us to limit ourselves and choose those solutions in which we feel confident – not necessarily choose those best suited to the job.
Nowadays, it is difficult to imagine an application without database. In some cases, the database is a pivotal element; one in the centre of the application. It may seem we have lots of choices in terms of database selection, but very often we tend to make this choice very superficially – instead of choosing between different types of persistence, we often choose between different relational database engines manufactured by Microsoft, Oracle or PostgreSQL.
Why does it happen? Why do we limit ourselves to relational databases only? Of course, there exists a set of situations in which relational databases are the best tool for the job, but – conversely – there exists a set of situations where relational database is a very inferior tool. Each type of tool has its purpose, limitations, and applications in which the tool will be the best.
The important thing is not to look at the application from the point of view of a database only. We need to look at the application as a whole, and then select an appropriate tool for the job – be it relational database or something else, perhaps tailored to a particular problem.
Relation-less databases:
Relational databases have reigned supreme continuously for last 20 years. The fact they aren’t very easy to use has been compensated by ORMs, but not everybody is aware of the fact that usage of ORMs is really an unconscious permission to kill the performance. On the bright side, it totally lifts the burden of being competent in the field of databases from us.
Those aren’t all problems of using relational databases. There are well-known issues of: Impedance Mismatch, Making changes, Consistency and efficiency, Strong typing, Normalization, Scalability which have to be addressed every time we work with this type of databases. Does it mean relational databases should never be used? Of course not, but it is not all roses and butterflies; there are trade-offs we need to be aware of.
Currently, it is difficult to imagine that one could choose something else than a relational database as the main data storage. However, some solutions fit well to relational databases, while some we are trying to put there by force.
This is like programming languages and frameworks, really. Theoretically, every problem could be solved in finite time using combination of C# (or Java) combined with MSSQL (or Oracle). Yet, other languages (and frameworks) have been created and used in commercial projects for example, Ruby (with Rails). Does it mean C# is obsolete? Or maybe Ruby is obsolete? Not really, those are different tools tailored to different purposes, like a screwdriver and a hammer. It gets even more complex when you combine different tools for different purposes in the same application for example, Front End of our web application can be written using HTML, JavaScript, ASP.NET. Backend part can be a Web Service created using C # and NHibernate. Yet, we will use only the same, single, relational database. Is the choice of a single type of database a good solution? Should we look for alternatives? Why should I learn something new when the old works and will give us the expected answer? Answer is quite simple: it depends.
From my perspective, a good example of a problem not fitting well with relational databases is, ironically, relationships. In the 21st century we are surrounded from all sides by graphs and all kinds of social networks. We can find them on social media, auction stores and book stores. Based on those networks, certain business decisions were made – what product should be recommended for us, what book should be read next etc.
These recommendations are made based on our activities and based on activities of people with whom we are in certain relationships. And this had to be done very fast, with performance being one of the key issues. To be able to resolve this type of a problem, companies such as Twitter, Facebook, Amazon and Google had to invent some new solutions which were better tailored to their needs. With the number of users constantly increasing, the amount of data has also increased rapidly and the existing databases no longer met their expectations.
NoSQL – addition, not replacement:
The NoSQL movement has risen to address some of the above sins. From the very beginning, NoSQL solutions were focused on high scalability and high availability. They have abandoned a rigid data model, which was characterized by relational databases in favour of easily extensible model without strong typing.
An important point here: neither NoSQL is, nor was intended to be an anti-SQL movement. It was supposed to be an alternate model, something different, designed to cope with different types of problems. NoSQL databases are also connected with the idea of multi-persistence – many different data storage depending on the current needs (analogously to the application with parts written in different languages presented earlier). So, if you need to store information about the network of friends, according to multi-persistence theory you should look for the appropriate database type, and not simply stuff everything into the main, well used relational database hoping that somehow everything will work smoothly.
Milgram Experiment – introduction:
Up to this point it has all been a theory, so let’s spice it with an example. To demonstrate in what way NoSQL database works better than relational in relation-type of a problem we will use an example of Milgram theory. The Milgram theory (named after Stanley Milgram), also known as the theory of six degrees of separation states that any two people on Earth are six (or fewer) acquaintance links apart.
According to this theory, if there are 30 people in lecture room and each of them has access to 100 other people, then we have access to a total of 3,000 people. On the second level of acquaintance relationship we have access to more or less 300,000 people. With each level of acquaintance the chance to reach the person we do not know personally (yet want to contact) grows. To summarize, Milgram theory states that in order to send a message to any unknown person who lives in any distant place we just have to use five intermediaries (or, in other words, intermediate nodes).
One of the variations of this theory ,and the one which will be considered from now on, is called Six Degrees of Kevin Bacon. In a way, this theory checks whether Milgram’s theory works with an existing well described network. In this case, a network of actors and movies in which they played. As the name suggests, every actor in this network would be tested against the connection with Kevin Bacon.
From the point of view of the data model, we are looking for an answer to the question whether there is a connection between Kevin Bacon and any other actor. If a particular actor did not play in the same movie as our hero (first degree), we should check whether he played in the same movie as other actors who have played with Kevin Bacon (second degree). If he did not, we should search other movies and actors over there. To be honest, it sounds more complicated than it actually is.
As some time ago I have managed to download from the Neo4j website a database containing information about actors and movies in which those actors had played (50125 actors, 12859 movies and 94700 connections between movies and actors.) I was able to test Six Degrees of Kevin Bacon. The reasoning and the experiment itself has been presented below using both relational database and graph database (one of NoSQL database types).
Milgram Experiment – Relational Model:
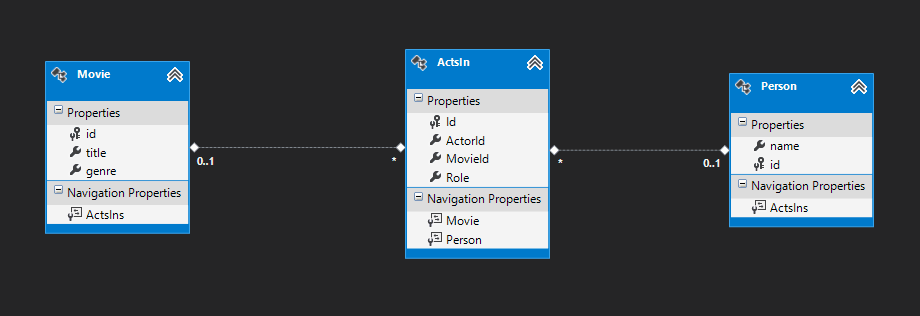
If you would like to create a model of Six Degrees of Kevin Bacon in a relational database, it would look as follows:
- Movies table stores information about Movies. Person table stores information about Actors.
- Most interesting element of this model is an ActsIn table which stores information about the relation linking Movies and Persons. One Person can act in multiple Movies. Many Persons could act in single Movie. So we have to introduce this table which represents a M:N relation.
The most common operations which this model supports are as follows:
- Check in which movies a particular actor has played,
- See who else played in the same movies.
Based on those two operations we are able to answer the question whether any two actors played together in the same movie, or whether an actor played in the same movie with any other actor, who played… well, let’s not complicate it further. It is as simple as a quote from one of „Weird Al” Yankovic’ songs „I know a guy who knows a guy who knows a guy who knows a guy who knows a guy who knows Kevin Bacon”.
In this model, verifying in which movies a particular actor has played would be very trivial:
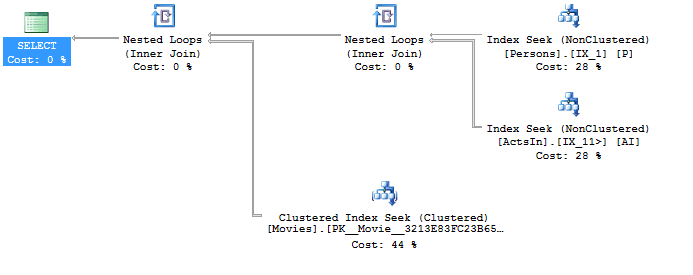
SELECT * FROM [dbo].[Persons] AS KevinBacon JOIN [dbo].[ActsIn] AS KevinBaconActsIn ON KevinBaconActsIn.ActorId = KevinBacon.Id JOIN [dbo].[Movies] AS KevinBaconsMovie ON KevinBaconActsIn.MovieId = KevinBaconsMovie.Id WHERE KevinBacon.[Name] = 'Kevin Bacon'
You should be aware that getting answer for this simple question requires two internal joins. With some well-defined covering indexes, we can see that the execution plan contains only seek operations.
This is not enough, though. To properly test Six Degrees of Kevin Bacon theory we will need a much larger number of joins. To see how many people were playing the same movies as Kevin Bacon would require another 2 internal joins. Every next level of acquaintance relationship requires us to extend the basic query to use the ever-growing number of joins. And to verify this theory we have to go deeper into the graph, up to 5 levels deep.
Within each level the number of people who play with the people you were playing with people (…) which played with Kevin Bacon will be ever greater. For such a small database performing operations on first level took me less than one second. But for the second level it was already above 10 seconds, for third level it took about 2 minutes. I finished experiment on the fifth level. It simply took over 1 hour without any apparent results.
The table ActsIn is used very often in this query. Thus, there exists a risk of very frequent locks. We have to perform up to four joins on each level and we have to visit ActsIn table twice per level.
To prove that this is a common problem, a similar experiment was performed by Partner and Vukotic. They performed experiments on social network which helped finding connections between friends (A problem known as “Friends of friends” problem). Maximal depth of this network was five. Question which they wanted to answer was whether there existed a path that connected two particular people. The number of people in the network was 1,000,000 with each person having approximately 50 friends.
In the table below you can find results of this experiment.
[table id=9 /]
The results come from the book „Graph Databases” by Ian Robinson, Jim Webber, Emil Eifrem.
Of course, some variations of SQL allow you to write recursive queries, but these do not improve the performance.
Milgram Experiment – NoSQL (Graph) database:
Although, in case of a graph database the basic data model allowing us to perform those operations contains only nodes and edges (which represent relationships), let’s expand it with additional types such as Actors, Movies and the relationship type ActsIn for the purpose of readability of this article.
I would like to mention language called Cypher, which is available in the Neo4j graph database. Cypher is a declarative language which can be used to express only our intentions while leaving the decision on how to realize our intentions to the database engine. From the point of view of a Cypher user, the user is interested only in getting information, not how the engine used its magic to deliver it.
One of the main features of the Cypher language is to find all paths that match the pattern we have described. Let’s look into the basic concept how to use this language:
- (variable:label) – a way to denote a node
- [variable:label] – a way to denote a relationship
- {key:value} – properties of a node or a relationship
The relationship between two nodes can be described as follows (A:Label)->(B:Label). In case of using this notation we are not interested in type of relationship between nodes, but we are interested in finding any existing path between those two nodes.
The relationship (A:Person)–[C:KNOWS]–(:Person) means that the two nodes are connected by the relationship of type KNOWS. If we put something before colon we will assign a variable name that way which can be used elsewhere in the query.
After colon, we can define the Type (which is a simple label). If we are not interested in using a variable or its type we can skip defining them. Labels, which represent the types of nodes and relationships, can be defined by the user; relationships should always have a type assigned. It should be remembered that both nodes and relationships are simply bags of properties and they can be used in other parts of the query as well, for example in the WHERE, RETURN statements.
To find Kevin Bacon in the graph we can write the following Cypher query:
MATCH p =(Kevin:Person)-[:KNOWS]-(friends:Person) WHERE Kevin.name = "Kevin Bacon" RETURN Kevin, friends
The MATCH phrase defines what we are looking for in the graph. We can describe a pattern that should be met by a part of graph.
In the WHERE clause we can define particular conditions that should be met by nodes or/and the relationships.
The RETURN clause allows us to return information.
Cypher gives us many ways to reach a particular goal. Like in Google Maps – we can simply ask for a way between points A and B, or we can specify particular points which are to be located on the way to be undertaken. The former case can be written as (A)-[*]>(B). The latter can (A)-[:KNOWS]->C-[:KNOWS]->(B)
The short summary given above shows just a small part of capabilities of Cypher language. Those should be enough to be able to follow the rest of article.
Having the basic knowledge of a Cypher language we are able to move on, to look at the graph database Neo4j. The graph database contains Actors, Movies and relationship that expresses that a given actor played in a movie. Neo4j provides several ways to operate and view the results of our operations based on graph database. A particularly interesting way is a visual access through the webpage which allows us to display results in form of a graph; that is, a picture.
Finding Kevin Bacon can be done in two different ways:
MATCH (a:Person) WHERE (a.name = "Kevin Bacon") RETURN a
Or
MATCH (a:Person { name : "Kevin Bacon"})
RETURN a
To display the movies in which Kevin Bacon has played we could run the following query:
MATCH (Kevin:Person)-[:ACTS_IN]->;(Movie:Movie) WHERE (Kevin.name = "Kevin Bacon") RETURN Kevin,Movie
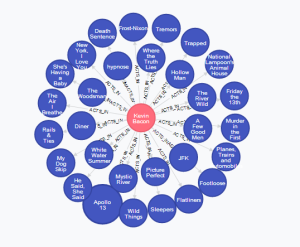
An interactive environment provided us by Neo4j enables us to present the data in the graph. In the following graph, each movie is represented by the blue circle, and each an actor (in this case Kevin Bacon) by the red circle.
To find the people that played in the same movies as Kevin Bacon we can use the following query:
MATCH (Kevin:Person)-[:ACTS_IN]->(Movie:Movie)<-[:ACTS_IN]-(Others:Person) WHERE (Kevin.name = "Kevin Bacon") RETURN Kevin, Movie, Others
As you can see a query written in Cypher will return only what we want to achieve. The screenshot above presents the whole response, but this response – unlike relational database having to create lots of tables when join operations took place - contains only a subset of the whole graph. The subset we were returned represents only the answer to a question we have asked. And Kevin Bacon is a central part of this graph.
As Winnie the Pooh used to say, "The farther into the forest, the more trees". To continue the experiment let’s check if the graph database makes it possible to find a link between any two actors in the graph above. In this example we will try to find connection between Kevin Bacon and another actor using intermediary actors.
To get the answer to this question, we must use pattern matching with variable path length. In this case the variable path can be defined as follows:
- (a:Person)-[:ACTS_IN*] -(c:Person)
Which means in English: get a list of all possible paths (which are paths of different lengths) to pass through the graph that match a pattern we have specified. If we wanted to get only the shortest path we would have to use the ShortestPath operator.
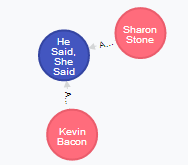
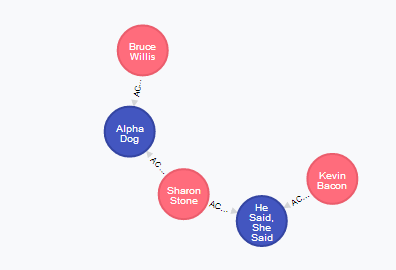
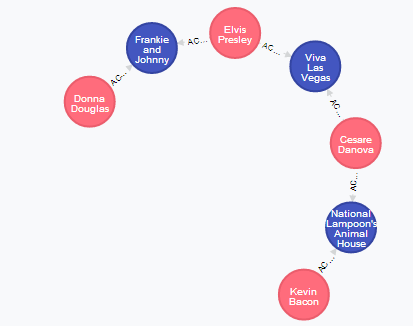
Below you can see the results of few experiments:
- Shortest path for Sharon Stone
- Shortest path for Bruce Willis
- Shortest path for Donna Douglas
- All connections between Kevin Bacon and Donna Douglas:
What was really striking was the performance of graph database compared to the performance of relational database. Finding the shortest path took about 3 seconds on a test environment while finding all paths that matched set patterns took about 80 seconds.
Summary
The goal of this article was to show that there are situations in which NoSQL databases are far superior to relational databases. It does not mean that relational databases are useless and from now on only NoSQL databases should be used to solve every problem in the world. On the contrary, relational databases are extremely useful tools having a wide range of applications.
One of the examples where SQL databases are superior to NoSQL ones is when it is necessary to assure data integrity – some NoSQL databases accept some potential loss of data integrity in return for improved performance.
But just like a single application can be built using a set of different programming languages depending on the role they are to fulfil, the same application can have a set of different persistency engines tailored to different needs. And graph databases are amazing tools for any domain, in which a graph is a natural way to represent the data model, like relations.